Mathematical mark-making

The natural beginnings of written mathematics start within children's imaginative play (Carruthers and Worthington, 2006; Worthington, 2009), yet confusion has surrounded the teaching of this aspect of mathematics. Whilst the Foundation stage emphasises that practitioners 'build on what children already know and understand' (QCA, 2000:11) it is clear that 'official' guidance has been sorely lacking on this important aspect of children's mathematical development and the pedagogy to support it. Research has shown that the abstract written language of mathematics causes significant problems for young chidlren and these continue to be identified by Ofsted. Our research has shown that in schools especially, children's early marks have been seldom recognised as mathematical, and their development has not been understood.

We originated the term children's mathematical graphics to describe the range of children's own mathematical marks and representations we found, through many years of research with children in the 2-8 year age-range (Carruthers and Worthington, 2006). Young children use scribble-marks, drawings, writing, invented (personal) and standard symbols to help them think about and communicate meanings. The following two examples are from children's self-initiated play.

Sam (3 years 6 months) had been watching his friend Bradley play with a calculator. As he pressed the buttons on the calculator, Bradley made marks on a piece of paper. Sam decided he wanted to join in and after he's played with a calculator for a while, reached for a pen and paper and made his own marks. During their play the boys chatted together occasionally and Bradley explained 'My dad's got one of these'. Sam and Bradley's social play and talk supported their thinking and encouraged Sam to join in with making marks that related to numbers - the first time he had done this.

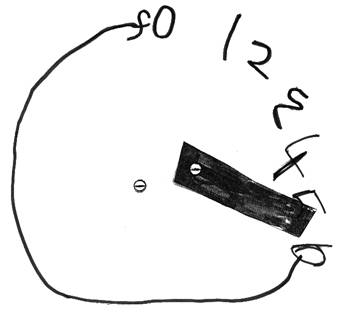
In Louisa's class the children had a limited number of choices for play each day. Louisa (4 years 9 months) was making what at first glance appeared to be a clock. When she explained how to use her dial, she assigned an activity to the numerals 1 - 5 that she had written, explaining: '1 - bricks; 2 - puzzles; 3 - role-play; 4 - reading; 5 - painting'. She paused with her finger on the '6', unable to think of other possibilities: then smiling, explained 'then you have a sleep!' Moving the hand on her dial to the letters 'fo' (off) she explained 'Where you turn it off'.

Louisa had related what she knew about clocks to her classroom culture. Perhaps she was making links with her home culture too, where after playing at the end of the day she goes to sleep.

Additional examples of children's mathematical graphics are in the Gallery here and here.

In your setting

Sometimes teachers and practitioners comment that they have been surprised to discover that some of the marks and representations children make are mathematical rather than marks of emergent writing. When you see a child making some marks think about the context in which the child has made them and watch and listen to what she says and does. Above all children will need to know that adults are genuinely interested in their marks and representations and what they intend them to mean.

Supporting children's own mathematical graphics should not imply young children sitting down to 'do written maths' - but learning environments where they choose to represent their mathematical thinking within authentic, child-initiated play. Children should also be free to choose how they represent their mathematical thinking for their purpose and context, and later for the calculation or problem they are solving.

Not 'recording'

Children's own representations support deep understanding by providing visual feedback, supporting their mathematical thinking, meanings and understanding about all aspects of written mathematics and symbols. In a sense children's mathematical graphics are their mental methods - on paper.

Recording what they did following a practical activity has limited value and involves lower levels of thinking. Children do not need to record mathematics they can do mentally, or to record something they have worked out in a practical context. Recording places the emphasis on marks and drawings as a product and is a lower level of cognitive demand (thinking) in mathematics. The difference between representing mathematical thinking and recording is one of quality and depth of thinking.

Processes of mathematical thinking (creative thinking, reasoning, meanings, understanding, problem solving, negotiation and co-construction of understanding) come to the fore in children's mathematical graphics, underpinning point 8 of the Foundation stage profile 'uses developing mathematical ideas and methods to solve practical problems' and many aspects of using and applying mathematics' (DfES, 2006). However, for many children the move to a new setting means an abrupt change in the way in which they are expected to write mathematics.

Transitions

Transitions have significant implications for young children's well-being and nursery schools and reception class teachers make considerable efforts to develop 'home-school' programmes to help integrate children and families into their next setting. The challenges of transitions have been widely recognised, (e.g. Brooker, 2002; Fabian and Dunlop, 2007; NFER, 2005; QCA, 2005). As Brooker emphasises, the culture of school is different and now children must 'learn to be a pupil'. But largely missing from the debate is curriculum transition (or continuity). The evidence is that children experience problem solving, reasoning and numeracy in especially contrasting ways, with expectations, opportunities and pedagogy in school that differ from nursery.

Researchers studying children's experiences in reception classes (Adams et al, 2004: 13) began with a view of young children 'as accomplished learners in their own right', yet their findings revealed an emphasis on 'the smallest building blocks of numeracy ... counting and number recognition' (p.85). Of greatest concern were 'the limited opportunities for sustained, shared, purposeful talk; for complex, imaginative play; and for authentic, engaging, first-hand experiences' (p. 27). Teachers in schools are now overwhelmed with multiple and complex pressures and we should all be concerned that these pressures are felt by the children for whom the play-based curriculum is planned. Play is the very best medium for the young child to develop and learn and is 'the curriculum the children have for themselves' (Paley, 2004: 20). More than ever before, children desperately need us to be advocates for play to be at the heart of their experience throughout the Foundation stage and through Year 1.

The 'Williams Maths Review'

The recently published 'Williams Maths Review' (WMR) on mathematics teaching in early years settings and primary schools, acknowledges the importance of children's mathematical graphics and makes specific recommendations on our work 'regarding early mark-making as a precursor to abstract mathematical symbolism' (DCSF, 2008: 4). The report includes our taxonomy of children's development from birth to 8 years, based on our analysis of 700 examples of children's mathematical graphics from our own teaching. This was the first time that this aspect of children's mathematical development had been charted. The taxonomy traces children's development from their early meaning making and explorations in play (including marks); through early written number and quantities to children's personal 'written' methods for calculations. Teachers and practitioners find the taxonomy helps them understand, appreciate and assess children's mathematical thinking; you can access it here.This is where the observations you make and examples of the children's mathematical graphics you collect can provide valuable insights. Assessing from a positive perspective will show you just how much the children already know and give you insights into their thinking.

Mathematical transitions

It is vital that teachers continue to build 'on what children already know and understand' about the written language of mathematics and support children's development in the reception class and in Key stage 1. But there are 'hidden' transitions to negotiate if children are to develop deep understanding and their own mathematical graphics have an important bridging function between concrete and mental operations, and between physical actions with concrete materials and the operations within written calculations (Carruthers and Worthington, 2008). Most significantly their own graphics enable children to bridge the divide between their early informal marks and the standard (abstract) written language of mathematics.

The WMR acknowledges that transition 'directly affects the young learner in mathematics'... 'Successful transition... requires full account to be taken of the child's accomplishments'...'Familiar approaches to children should (also) be maintained in Year 1', and encourages teachers in Year 1 'to increase opportunities for 'learning through play' (DCSF, 2008: 40, 41). Children's own mathematical marks and representations can support them over time, from recognising that their earliest scribble-marks can carry mathematical meanings, to understanding the specific meanings of standard symbols such as '+' and layouts of calculations at a deep level. They develop meaningful personal written methods; choose appropriate ways to represent data and strategies they understand to solve mathematical problems. They can provide continuity of experience for children through the Foundation stage and Key stage 1.

Conclusion

Stephenson and Parsons explain that the 'notion that early years education in England covers the age range 3-5 years' (now birth-5), 'is not helpful'... Children in Key Stage 1 'who are aged 5-7 years, are as much 'early years' as their peers in Reception classes' (Stephenson and Parsons, 2007: 142). The greatest changes have been found in the transition into Year 1, 'where children often wait to be told what to do next, and have set subjects according to the teacher's agenda' (Fabian and Dunlop, 2005: 239). Fabian and Dunlop emphasize that it is helpful if changes are 'continuous rather than abrupt, if connections are emphasized and environments and modes of learning are similar' (2005: 234). Children's mathematical graphics should not be restricted to either the nursery or the Foundation stage and like emergent writing there should be a seamless development (i.e. a continuous 'building on') from their earliest marks in play so that children experience 'continuity' in their 'written' mathematics. The WMR recommends that:

To secure effective pedagogy, local authorities, leaders, managers and head teachers should provide the following key elements of support in order for all settings to develop the conditions for learning...

• A culture with a significant focus on mathematical mark-making in line with early writing, through, for example, role-play and the use of popular mathematical signage in the environment
• A learning environment that encourages children to choose to use their own mathematical graphics to support their mathematical thinking and processes' (2008: 37).

'Mathematical signage' might include a list of children's or adults' choices for drinks (how many for each); a note from a child's parent about the time of her son's dental appointment, or a sign you write giving the time that the photographer will be visiting your class. The important point about all of these signs is that their messages are real - about genuine choices and real people, appointments and times that are relevant to the children in your setting or class. Just as providing environmental print 'models' and encourages children to write, displaying mathematical print will encourage children to make their own mathematical marks. To support these you will want to include number lines and other mathematical print.

Returning to the issue of transitions, the WMR argues for 'a coherent progression from EYFS to Year 1' (DCSF, 2008: 63). Developing children's mathematical graphics throughout the Foundation stage and Key stage 1 will ensure that they develop a good understanding of the written language of mathematics. It will also ensure continuity in written mathematics as children move from nursery to the reception class and later, into Key Stage 1.

In these recommendations the authors of the 'Williams Review' have done a great service to young children's mathematical potential that is likely to have implications for greater understanding and continuity for their mathematics. Perhaps at last we will see a more 'playful pedagogy'* that is in tune with children's development and strengths and contributes to continuity in the children's mathematical curriculum.

* 'Playful pedagogy', (Moyles: 2005: 😎

________________________________________________________________

Maulfry Worthington is currently engaged in research for her doctorate (Free University, Amsterdam) on the beginnings of children's mathematical graphics in imaginative play.

The Children's Mathematics Network

In 2003 we founded the Children's Mathematics Network as a 'grassroots' network for teachers and practitioners to support children's mathematical graphics. There are several ways in which you may find this helpful, including setting up your own 'Children's Mathematics Network Group' in your locality and becoming a member.

________________________________________________________________

Further articles and publications by Carruthers and Worthington - some downloadable.

References

Adams, S., Alexander, E., Drummond, M. J. and Moyles, J. (2004) Inside the Foundation Stage: Recreating the Reception Year, London: Association of Teachers and Lecturers (ATL).

Brooker, L. (2002) Starting School: Young Children Learning Cultures, Buckingham: Open University Press.

Carruthers, E. and Worthington, M. (2006) Children's Mathematics: Making Marks, Making Meaning. London: Sage Publications, (2nd Ed.).

Carruthers, E. and Worthington, M. (2008) 'Children's mathematical graphics: young children calculating for meaning' in I. Thompson, (Ed.) (2008) Teaching and Learning Early Number, Maidenhead: Open University Press, (2nd Ed.).

DCSF (2008) The Final Report of the Independent Review of Mathematics Teaching in Early Years Settings and Primary Schools, London: DCSF, (June 2008) Chapter 3: The Early Years.

DfES (2006) 'Guidance Paper: Using and Applying Mathematics', London: DfES.

Dunlop, A-W., and Fabian, H. (Eds.) (2007) Informing Transitions in the Early Years: Research, Policy and Practice. Maidenhead: OU Press.

Fabian, H. and Dunlop, A-W. (2005)'The importance of play in the transition to school', in J. Moyles, (Ed.) The Excellence of Play, Maidenhead: Open University Press.

Moyles, J. (Ed.) (2005) The Excellence of Play, Maidenhead: OU Press, (2nd Ed.)

Paley, V. G. (2004) A Child's Work: the Importance of Fantasy Play, Chicago: The University of Chicago Press.

Sanders, D., White, G., Burge, B., Sharp, C., Eames, A., McEune, R. and Grayson, H. (2005) A Study of Transition from the Foundation Stage to Key Stage 1, NFER Research Report.

Stephenson, M. and Parsons, M. (2007) ‘Expectations: effects of curriculum change as viewed by children, parents and practitioners' in A-W. Dunlop and H. Fabian., (Eds.) (2006) Informing Transitions in the Early Years: Research, Policy and Practice. Maidenhead: OU Press.

QCA (2000) Curriculum Guidance for the Foundation Stage, London: DfES / QCA.

QCA (2005) Continuing the Learning Journey: INSET package, London: QCA.

Worthington, M. (2009) 'Play is a complex landscape: imagination and symbolic meanings'; in P. Broadhead, L. Wood, and J. Howard. (Eds) Play and Learning in Educational Settings, London: Sage Publications, (in preparation).